
La natura del radar
Il radar (da RAdio Detection And Ranging), e’ un sensore radio, generalmente (ma non sempre) operante nella banda delle microonde (> 1 GHz), di tipo ATTIVO. Attivo significa che il sensore emette energia (in questo caso un’onda elettromagnetica) verso l’ambiente circostante, e ricava informazioni su tale ambiente analizzandone l’eco di ritorno.
Nel caso specifico, e’ possibile determinare la posizione di oggetti :
- In azimuth/elevazione, grazie alla direttività dell’antenna : se si dispone di un’antenna direttiva, si riceverà ovviamente l’eco solo quando si irradia in direzione di esso.
- In distanza, misurando il ritardo dell’eco, essendo nota la velocità della luce (circa 3×10^8 m/sec). In 1 microsec, l’onda elettromagnetica percorre quindi 300 m : considerando che essa deve percorrere la distanza in andata ed in ritorno, un ritardo di 1 microsec corrisponde quindi ad una distanza dell’oggetto di circa 150 metri.
La maggior parte dei radar sono del tipo cosiddetto monostatico, cioè hanno il trasmettitore ed il ricevitore fisicamente uniti in un unico apparato: di converso sono possibili radar bistatici o multistatici, in cui vi sono un trasmettitore ed uno o più ricevitori fisicamente separati.
Per inciso, il primo radar sperimentale di Watson-Watt (1937) era di tipo bistatico : infatti vi erano un trasmettitore ed un ricevitore distanti alcune centinaia di metri : il ricevitore rivelava una variazione del segnale ogni qualvolta un aereo sorvolava lo spazio tra trasmettitore e ricevitore, dimostrando cosi’ la fattibilità di avvistare oggetti volanti tramite onde radio.
I radar più comunemente impiegati sono del tipo ad impulsi : il segnale trasmesso e’ un “breve” (dove per breve si intende, da decine di nanosec a decine di microsec) impulso di radiofrequenza, ripetuto periodicamente.
Durante l’intervallo tra un impulso trasmesso e l’altro, l’apparato commuta
in ricezione (normalmente, impiegando la stessa antenna utilizzata per
la trasmissione) per captare gli echi di ritorno.
Portata non ambigua
Quando si parla di portata di un radar, occorre distinguere tra portata
non ambigua e portata effettiva.
La portata non ambigua e’ (sempre riferendoci al caso classico di radar ad impulsi) legata alla frequenza di ripetizione degli impulsi stessi (PRF = Pulse Repetition Frequency, l’inverso e’ il PRI = Pulse Repetition Interval).
Un tipico timing di un radar e’ illustrato in fig 1 : due impulsi di trasmissione successivi (chiamati Tx 1 e Tx 2) sono separati da una distanza pari al PRI. L’eco Rx 1 e’ l’eco dell’impulso Tx 1 riflesso da un bersaglio che si trova ad una distanza “Range A”. L’eco Rx 2 potrebbe essere dovuto sia ad una riflessione dell’impulso Tx 2 da un bersaglio che si trovi a distanza “Range B”, sia ad un bersaglio più lontano (“Range C”), che riflette l’impulso precedente.
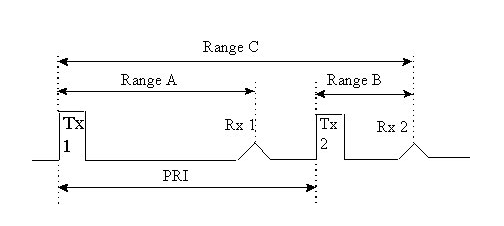
In quest’ultimo caso si dice che il bersaglio si trova in distanza ambigua.
La massima portata non ambigua del radar e’ quella corrispondente alla
PRI, cioè :
Rna = PRI c / 2
Nota : e’ possibile discriminare comunque la distanza effettiva di oggetti posti a distanza superiore a quella ambigua alternando frequenze di ripetizione di impulsi diverse.
L’oggetto che si trovi a distanza ambigua avrà distanze apparenti diverse per ogni diversa PRI. Un’apposita logica e’ quindi in grado di risolvere l’ambiguità, determinando la distanza reale. Il problema non si pone in genere per i radar impiegati, p.es., per l’osservazione della terra dallo spazio : in questo caso, ci si attendono echi solo in una ristretta fascia di distanza (la distanza del satellite tra i punti della superficie illuminati più vicino e più lontano), in quanto non ci si aspetta nessun oggetto tra il radar e la superficie terrestre.
In questo caso l’ambiguità e’ nota a priori e non richiede tecniche
particolari per essere risolta.
L’Equazione Radar
La portata non ambigua, in realtà, non da nessuna indicazione sulla capacita di un radar di rilevare un oggetto ad una determinata distanza : essa indica solo la massima distanza a cui una eventuale eco ricevuta può essere correttamente interpretata. Per determinare la portata effettiva occorre considerare la perdita della tratta (anzi, delle tratte, radar-bersaglio e bersaglio-radar) e le caratteristiche del bersaglio. Il rapporto segnale/rumore (da qui in poi, S/N) minimo richiesto per la corretta detezione di un bersaglio, dipende dalle modalità di elaborazione del segnale ed è qui supposto fissato a priori, in quanto una trattazione
dell’argomento richiederebbe eccessivo spazio.
NOTA : pur non entrando qui nel dettaglio dell’argomento, e’ importante
sottolineare come la detezione radar sia sempre un fenomeno statistico.
Il problema fondamentale e’ quello di discriminare la presenza di un segnale immerso in un rumore avente distribuzione gaussiana. Comunque posizioni la mia soglia di decisione (“tutto ciò che supera la soglia e’ segnale,
tutto ciò che sta sotto e’ rumore”) vi e’ sempre una probabilità finita che : 1) il rumore superi la soglia o 2) il segnale + il rumore siano al disotto della soglia (anche se il segnale da solo sarebbe stato al di sopra). Per un dato rapporto S/N e’ possibile, variando la soglia, ridurre la probabilità di falso allarme a scapito della probabilità di detezione e viceversa. Per cui non sarebbe corretto dire “il radar ha una portata di x chilometri sul bersaglio y”, a meno di non aggiungere “con 90% di probabilità di detezione e probabilità di falso allarme 10^-6).
Senza derivare qui l’intera equazione radar, cerchiamo di illustrare alcuni
concetti fondamentali.
Immaginiamo di avere un’antenna trasmittente isotropica, cioè che irradi omogeneamente in tutte le direzioni. La potenza trasmessa Pt, ad una distanza R dal trasmettitore, sarà distribuita omogeneamente sulla superficie di una sfera di raggio R, con una densità di potenza
Pd = Pt / (4 pi R^2)
Tutte le antenne reali sono però di tipo direttivo : il guadagno di antenna (numero puro, indicato con G) indica quanto l’antenna stessa sia “efficace” nel concentrare l’energia nella direzione di interesse (a scapito ovviamente di quella irradiata in altre direzioni)
Pd = G Pt / (4 pi R^2)
Nel caso di un bersaglio puntiforme (e’ considerato puntiforme un oggetto le cui dimensioni siano piccole rispetto alla risoluzione in angolo e in distanza – del radar. P. es., per un radar di avvistamento tipico, un Boeing 747 e’ un bersaglio puntiforme), le caratteristiche dell’oggetto bersaglio entrano in gioco tramite il parametro di riflettività (cross-section), indicato con sigma (misurato in m^2). Un oggetto con sigma = 1 m^2 riflette verso il radar una potenza equivalente a quella di un riflettore che reirradi isotropicamente tutta la potenza incidente su 1 m^2 di superficie (va da sé che l’oggetto potrebbe essere più piccolo ma reirradiare prevalentemente nella direzione di incidenza del segnale).
NOTA : nel caso di bersagli estesi (p. es., superfici di terreno o di oceano) la riflettività (chiamata, in questo caso, sigma-zero) è un numero puro, avente come riferimento una superficie di eguale area che reirradiasse isotropicamente tutta l’energia incidente.
Per il segnale di ritorno dal bersaglio al radar, vale esattamente lo stesso ragionamento fatto per il segnale di andata : la potenza di ritorno al radar si distribuisce sulla superficie della sfera : la densità di potenza in ricezione sarà così :
Pr = Pt G sigma / (16 pi^2 R^4)
Il segnale viene catturato dall’antenna ricevente, in proporzione alla sua area equivalente. Se usiamo la stessa antenna per la trasmissione e per la ricezione, ci torna comodo la formula che lega l’area equivalente al guadagno :
G = 4 pi / (lambda^2) Aeff
La potenza che ritorna al ricevitore radar sarà così :
Pr = G^2 Pt sigma lambda^2 / (64 pi^3 R^4)
Nota : questa formula non tiene conto per semplicità delle perdite per attenuazione atmosferica ne di quelle dovute alla non idealità del sistema.
La cosa più importante da notare è che la potenza ricevuta decresce con la quarta potenza della distanza : per poter incrementare la portata di un fattore 2 occorre aumentare la potenza trasmessa di ben 16 volte ! (Questo sempre nel caso di un bersaglio puntiforme : se il bersaglio è, p.es., una superficie, occorre tener conto che il fascio di antenna si “apre” con la distanza, incrementando l’area della cella di risoluzione, e quindi la potenza riflessa. A seconda della geometria radar-superficie, il segnale di ritorno può essere proporzionale a 1/R^3 o ad 1/R^2.)
Il segnale di ritorno si trova a competere, nel ricevitore, con il rumore
termico, la cui potenza (potenza equivalente all’ingresso del ricevitore)
è data da :
Pn = kT B F
dove :
k = costante di Boltzmann
T = temperatura del ricevitore in gradi Kelvin
B = Banda di rumore del ricevitore (in prima approssimazione uguale alla sua banda passante)
F = Figura di rumore, termine maggiore di 1 che indica quanto la rumorosità del ricevitore stesso sia peggiore rispetto al caso ideale
Può così essere calcolato il rapporto segnale-rumore.
E’ importante notare come il rumore del ricevitore sia proporzionale alla
sua banda passante. Ciò è anche abbastanza intuitivo in quanto il rumore termico è “bianco”, cioè distribuito omogeneamente su tutte le frequenza. All’aumentare della banda aumenta quindi la quantità di rumore presente all’uscita del ricevitore. E’ quindi fondamentale che la banda del ricevitore sia la più stretta possibile, compatibilmente con la necessità di amplificare correttamente il segnale. Nel caso di un semplice impulso su portante la banda ottimale è circa B = 1/T (dove T è la durata dell’impulso).
Dal punto di vista della portata appare quindi conveniente, a pari potenza
di picco, aumentare la durata dell’impulso trasmesso (e quindi, la sua
energia). Questo è però in contrasto con le esigenze di risoluzione in distanza, come si vedrà tra breve.
Generalizzando al caso di segnali diversi dal semplice impulso su portante,
è possibile dimostrare che la portata è legata esclusivamente all’energia dell’impulso, cioè al prodotto P x T, a condizione che il ricevitore impieghi un filtro “ottimo” (detto filtro adattato), caratterizzato da avere una risposta in frequenza che sia complessa coniugata dello spettro del segnale (ovvero, stessa risposta in ampiezza dello spettro del segnale, fase opposta).
Risoluzione in angolo ed in distanza
La risoluzione in angolo corrisponde, per un radar di tipo convenzionale,
all’apertura del fascio di antenna. Questa dipende dalle dimensioni lineari
dell’antenna stessa e dalla lunghezza d’onda del segnale. Per un’antenna
avente dimensione l, l’apertura del fascio (in radianti) può essere determinata in via approssimata dalla formula
theta = 1.2 lambda / l
Utilizzare frequenze più elevate presenta quindi il vantaggio di poter impiegare antenne di minori dimensioni a parità di risoluzione angolare.
Per quanto riguarda la risoluzione in distanza, è possibile discriminare tra di loro due echi se la differenza dei loro ritardi è maggiore della durata T degli impulsi stessi. La risoluzione in distanza è quindi pari a T c/2.
Per ottenere una migliore risoluzione in distanza, è quindi necessario accorciare l’impulso, allargandone la banda (si dimostra che il contenuto informativo, in questo caso la risoluzione in distanza, è proporzionale alla banda del segnale) : questo però equivale a diminuirne l’energia, riducendone quindi la portata a parità di altre condizioni.
Ciò pone notevoli difficoltà nella realizzazione di radar aventi risoluzioni spinte : infatti, il limite tecnologico nella realizzazione dei trasmettitori è relativo soprattutto alla potenza di picco, piuttosto che alla potenza media e all’energia del singolo impulso. In pratica, un trasmettitore che eroghi un impulso da 2 kW di picco per 10 microsec è molto più facile da realizzare di uno che emetta 20 kW per 1 microsec, anche se l’energia dell’impulso rimane la stessa.
Per conciliare l’esigenza di elevate risoluzioni in distanza con l’impiego di impulsi “lunghi” con limitata potenza di picco, si ricorre spesso alla cosiddetta codifica dell’impulso. Tale tecnica consiste nell’introdurre una qualche forma di modulazione in un impulso di lunga durata, allargandone la banda. In questo modo è possibile distinguere due echi parzialmente sovrapposti grazie alla modulazione presente nell’impulso.
La risoluzione in tempo di un sistema del genere è in prima approssimazione pari a T’ = 1/B (che nel caso di un impulso non modulato di durata T, avendo questo una banda 1/T, si riduce a T’ = T).
I due tipi di modulazione più usati in queste applicazioni sono quella cosiddetta chirp ed il Codice di Barker : la prima è una modulazione lineare di frequenza, il secondo una modulazione discreta bifase.
In ricezione, il segnale viene correlato con una replica del segnale trasmesso memorizzata nel sistema. Nel caso del chirp, p.es., ciò può essere effettuato facendo transitare il segnale (normalmente, nella sezione a frequenza intermedia del ricevitore) in una linea di ritardo acustica dispersiva, avente cioè ritardo variabile in funzione della frequenza, in grado quindi di concentrare tutta l’energia in un impulso più corto. Sfruttando le moderne tecniche di elaborazione digitale del segnale, è anche possibile, dopo aver convertito il segnale ricevuto in forma digitale, effettuarne il prodotto di convoluzione con una eco puntiforme ideale (generalmente ciò viene fatto operando nel dominio della frequenza dopo avere fatto la trasformata di Fourier del segnale, essendo meno pesante dal punto di vista computazionale).
Per il codice di Barker, si possono utilizzare linee di ritardo a prese intermedie con una rete di somma e pesatura in fase. Ciò può venire realizzato sia in digitale sia in analogico (a frequenza intermedia) utilizzando sempre una linea di ritardo acustica (non dispersiva).
Effetto Doppler
L’effetto Doppler è ampiamente sfruttato da svariati tipi di radar
per estrarre informazioni sulla velocità radiale dei bersagli (in
particolare da tutti quelli, civili o militari, destinati a rilevare bersagli
aerei, per discriminare gli stessi dagli echi fissi).
Un segnale di lunghezza d’onda lambda emesso da una sorgente, è
percepito da un ricevitore che si trovi in moto relativo con velocità
radiale v come spostato in frequenza di una frequenza pari a v/lambda rispetto al segnale emesso.
Nel caso radar l’effetto occorre due volte, sulle tratte radar-bersaglio
e bersaglio-radar : lo spostamento doppler è quindi pari a:
delta -f = 2 v / lambda
Da notare che alle normali frequenze radar, e per velocità dell’ordine
delle decine, o al massimo, centinaia di m/sec (come gli aeroplani), lo spostamento doppler è dell’ordine dei kHz, confrontabile con le PRF dei radar stessi, e con periodo molto più grande della durata degli impulsi stessi. Risulta quindi impossibile discriminare la doppler all’interno dell’impuso.
Tutti i radar che utilizzano l’informazione doppler impiegano gli stessi oscillatori di riferimento (dotati di elevata stabilità a breve termine) sia in trasmissione che in ricezione . L’oscillatore locale LO1 è lo stesso per entrambe le catene. Il segnale ricevuto, anziché essere demodulato tramite un rivelatore di ampiezza, viene
confrontato (in genere su due canali sfasati di 90° per estrarre le componenti seno e coseno del segnale) con la frequenza di riferimento di trasmissione LO2 – usata per generare l’impulso trasmesso a frequenza intermedia
– tramite un discriminatore di fase (in pratica, un mixer bilanciato dotato di basso offset).
L’ampiezza del segnale di uscita dipende, oltre che dall’ampiezza del segnale di ingresso, anche dalla differenza di fase tra questo e il riferimento (la frequenza del segnale di uscita è, a meno dello spostamento doppler, zero, perché le frequenze degli oscillatori in trasmissione e ricezione si cancellano).
Un impulso di ritorno da un oggetto fisso avrà doppler zero, quindi fase costante : tutti gli impulsi demodulati avranno la stessa ampiezza. Se è presente uno spostamento doppler, la fase varierà da impulso ad impulso, e così pure l’ampiezza del segnale demodulato.
Utilizzando un demodulatore a due canali (seno e coseno), è possibile ricostruire in maniera non ambigua la fase del segnale di ritorno.
In pratica, è come se l’inviluppo doppler del segnale si trovasse ad essere campionato alla frequenza di ripetizione di impulso. Per evitare ambiguità nella misura della doppler è quindi necessario, in accordo col teorema del campionamento, che la PRF sia almeno doppia della massima doppler attesa.
Ciò è in contrasto col requisito di portata massima non ambigua descritto in precedenza. Le relative tecniche di risoluzione di ambiguità permettono, in parte, di conciliare i due requisiti. (E’ comunque da notare che in molti radar, l’ambiguità in doppler non costituisce un problema, in quanto lo spostamento doppler non è usato per una misura di velocità ma solo per discriminare – eliminandoli dalla presentazione – i bersagli al disotto di un certo spostamento – gli echi fissi. In questo caso l’unico problema posto dall’ambiguità in doppler è che un bersaglio con doppler multipla intera della PRF viene visto a fase costante – doppler nulla – e quindi cancellato come se fosse un’eco fissa).
Ove occorra una accurata misura della frequenza Doppler, si possono impiegare radar in onda continua (CW). Tali radar non forniscono però nessuna informazione sulla distanza. Radar di questo tipo, ma con moderata capacità di discriminazione in distanza grazie ad una modulazione in frequenza della portante (radar FM-CW), sono impiegati per applicazioni particolari (radar guida missili).



